2024-TSCTF-J-partWP-crypto

2024-TSCTF-J-partWP-crypto

出了五道入门密码题，非常荣幸，写一下题解。

ezRSA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
from Crypto.Util.number import *
import base64
from secret import flag
import os
encoded_flag = base64.b64encode(flag)
part_length = len(encoded_flag) // 4
parts = [encoded_flag[i:i + part_length] for i in range(0, len(encoded_flag), part_length)]

#part1
p = getPrime(512)
q = getPrime(512)
n = p * q
phi = (p-1) * (q-1)
d = getPrime(250)
e = inverse(d, phi)
c = pow(bytes_to_long(parts[0]), e, n)
print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
'''
n = 124695452995031270645183837267530422032624508784074534979189655228220709056309638648794696369835930482818980808128467814617220810217534821336503942838791498456112882717378013827550680516551959078234339477401303759763506487676709408813412867364414651706461400252466842182365340612883444737530603407481042520627
e = 38587713366842463962841747677614707312145479235042165803103947138237921458583509748629042842505955223421671992698976799249425980974893271454942323501453571320592126625468760278770909411858284131095166550317734018153286242950401311537208914820833671566620645882329390747892971373265592565291598852744678229891
c = 75650426098322108299742769179799276679353245586432433359812352366165787480762021753671012472067826915659840541954505167382050569833945309043431554352347482992118091659840982421987700648585142917347916194810259117115753813661282178558428786374835684668840019166776178494086580424196110694158066034697988927644
'''

#part2
p = getPrime(80)
q = getPrime(80)
n = p * q
e = 2
c = pow(bytes_to_long(parts[1]), e, n)
print(f'n = {n}')
print(f'c = {c}')
print(f'p,q = {p,q}')

'''
n = 649329048322675374317593820985753646586809799201
c = 283668420132846011615755415362202578109404366325
p,q = (647260709632957671018359, 1003195526406802286444839)
'''

#part3
p = getPrime(512)
q = getPrime(512)
n = p * q
e = 65537
c = pow(bytes_to_long(parts[2]), e, n)
print(f'n = {n}')
print(f'c = {c}')
print(f'p^q = {p^q}')
'''
n = 85836893651204560884454211125508692415276042143801480450535044733242333318334455339451808653755272841343378345709375676280488068099971805717946097641116078266013229365158341178806480395974457905053516603153056936745020102883744430977333247681929718298626185526512756702624513738698825219177049538628421559753
c = 75578834548096799626696300881096262997184146142305165096930004492293642496308047534319034721187289042138332386120962890635270628767192988167590315544321566944902760623837249074921079890026503778053466720161607743010204269544291059577848021218234039433294700788160167294093796603060247381385159054508170520277
p^q = 5068548570505625142069285468439450186210992627026138517591800598908379828953823253346928574075223127205617451260708785889033493211347183583859669806824864
'''

#part4
p = getPrime(512)
q = getPrime(512)
n = p * q
e = 3
m = bytes_to_long(os.urandom(32)+parts[3])
c = pow(m, e, n)
print(f'n = {n}')
print(f'c = {c}')
print(f'mleak = {m>>128}')
'''
n = 136909292741753142871542219643510188168311518562065789353531367466023357011784735447560466352669948897633633920102617017949126915203615330337196942328793619163571419292670395849251337340787480297972818664454785647844715189207055430597030032696044932960884594660634280475822683286430432169515120767378120972393
c = 14763067643592454478187771324072634160297758439803081056226124797870386993054732731754324146768654813122274647054179017048620683751626439261028839186682159969656271385676822426489416369402998625865982105676257668946313225156476831065481561281126267398712822218497384996243578386630794573662378684549962709522
mleak = 287621732882458207416007037901690948810437972193283953524078189541847647258
'''


板子题，维纳攻击，Rabin，pq异或剪枝，coppersmith已知部分m

具体的都可以在网上找到非常非常详细的解释，这题确实也是为了让大家学会搜索而出的题目。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
from Crypto.Util.number import *
import base64
import os
import gmpy2

#part1 wiener attack
def transform(x,y):       #使用辗转相处将分数 x/y 转为连分数的形式
    res=[]
    while y:
        res.append(x//y)
        x,y=y,x%y
    return res
    
def continued_fraction(sub_res):
    numerator,denominator=1,0
    for i in sub_res[::-1]:      #从sublist的后面往前循环
        denominator,numerator=numerator,i*numerator+denominator
    return denominator,numerator   #得到渐进分数的分母和分子，并返回

    
#求解每个渐进分数
def sub_fraction(x,y):
    res=transform(x,y)
    res=list(map(continued_fraction,(res[0:i] for i in range(1,len(res)))))  #将连分数的结果逐一截取以求渐进分数
    return res

def get_pq(a,b,c):      #由p+q和pq的值通过维达定理来求解p和q
    par=gmpy2.isqrt(b*b-4*a*c)   #由上述可得，开根号一定是整数，因为有解
    x1,x2=(-b+par)//(2*a),(-b-par)//(2*a)
    return x1,x2

def wienerAttack(e,n):
    for (d,k) in sub_fraction(e,n):  #用一个for循环来注意试探e/n的连续函数的渐进分数，直到找到一个满足条件的渐进分数
        if k==0:                     #可能会出现连分数的第一个为0的情况，排除
            continue
        if (e*d-1)%k!=0:             #ed=1 (mod φ(n)) 因此如果找到了d的话，(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)
            continue
        
        phi=(e*d-1)//k               #这个结果就是 φ(n)
        px,qy=get_pq(1,n-phi+1,n)
        if px*qy==n:
            p,q=abs(int(px)),abs(int(qy))     #可能会得到两个负数，负负得正未尝不会出现
            d=gmpy2.invert(e,(p-1)*(q-1))     #求ed=1 (mod  φ(n))的结果，也就是e关于 φ(n)的乘法逆元d
            return d
    print("该方法不适用")
    
    
n = 124695452995031270645183837267530422032624508784074534979189655228220709056309638648794696369835930482818980808128467814617220810217534821336503942838791498456112882717378013827550680516551959078234339477401303759763506487676709408813412867364414651706461400252466842182365340612883444737530603407481042520627
e = 38587713366842463962841747677614707312145479235042165803103947138237921458583509748629042842505955223421671992698976799249425980974893271454942323501453571320592126625468760278770909411858284131095166550317734018153286242950401311537208914820833671566620645882329390747892971373265592565291598852744678229891
d=wienerAttack(e,n)
c = 75650426098322108299742769179799276679353245586432433359812352366165787480762021753671012472067826915659840541954505167382050569833945309043431554352347482992118091659840982421987700648585142917347916194810259117115753813661282178558428786374835684668840019166776178494086580424196110694158066034697988927644
print("d=",d)
part1 = long_to_bytes(pow(c,d,n))
print(part1) #b'VFNDVEYtSnsiclN'

#part2 rabinRSA
n = 649329048322675374317593820985753646586809799201
c = 283668420132846011615755415362202578109404366325
p,q = (647260709632957671018359, 1003195526406802286444839)
mp = pow(c,(p+1)//4,p)
mq = pow(c,(q+1)//4,q)
#   sp+tq=1  
s = gmpy2.invert(p,q)   # (p^-1) mod q 
t = gmpy2.invert(q,p)   # (q^-1) mod p
x = (t*q*mp+s*p*mq)%n
y = (t*q*mp-s*p*mq)%n
 
print([long_to_bytes(v%n) for v in [x,-x,y,-y]])#b'hXzFzX2MwbXBMZX'

#part3 p^q

def get_pq(n, x):
    a = [0]
    b = [0]
    maskx = 1
    maskn = 2
    for i in range(1024):
        xbit = (x & maskx) >> i
        nbit = n % maskn
        t_a = []
        t_b = []
        for j in range(len(a)):
            for aa in range(2):
                for bb in range(2):
                    if aa ^ bb == xbit:
                        tmp2 = n % maskn
                        tmp1 = (aa * maskn // 2 + a[j]) * (bb * maskn // 2 + b[j]) % maskn
                        if tmp1 == tmp2:
                            t_a.append(aa * maskn // 2 + a[j])
                            t_b.append(bb * maskn // 2 + b[j])
        maskx *= 2
        maskn *= 2
        a = t_a
        b = t_b
    for a1, b1 in zip(a, b):
        if a1 * b1 == n:
            return a1, b1
n = 85836893651204560884454211125508692415276042143801480450535044733242333318334455339451808653755272841343378345709375676280488068099971805717946097641116078266013229365158341178806480395974457905053516603153056936745020102883744430977333247681929718298626185526512756702624513738698825219177049538628421559753
c = 75578834548096799626696300881096262997184146142305165096930004492293642496308047534319034721187289042138332386120962890635270628767192988167590315544321566944902760623837249074921079890026503778053466720161607743010204269544291059577848021218234039433294700788160167294093796603060247381385159054508170520277
pq = 5068548570505625142069285468439450186210992627026138517591800598908379828953823253346928574075223127205617451260708785889033493211347183583859669806824864
#print(get_pq(n,pq))
p,q = (7071885161396583396463096463625209044303327972167708438066857001830332768701746624020834805511703081047126757150658001950574691764834038852771215770021517, 12137766902630692204014930687092692421705024861458681276005451698346350903669687744428609039166970461294162324174541673034447500506353559460507837247083309)
print(long_to_bytes(pow(c,gmpy2.invert(65537,(p-1)*(q-1)),n)))#b'hfQnVUX0V6X3QwX'

#part4 coppersmith **in sagemath**
n = 136909292741753142871542219643510188168311518562065789353531367466023357011784735447560466352669948897633633920102617017949126915203615330337196942328793619163571419292670395849251337340787480297972818664454785647844715189207055430597030032696044932960884594660634280475822683286430432169515120767378120972393
c = 14763067643592454478187771324072634160297758439803081056226124797870386993054732731754324146768654813122274647054179017048620683751626439261028839186682159969656271385676822426489416369402998625865982105676257668946313225156476831065481561281126267398712822218497384996243578386630794573662378684549962709522
mleak = 287621732882458207416007037901690948810437972193283953524078189541847647258
m = mleak<<128
PR.<x> = PolynomialRing(Zmod(n))
f = (m + x)^3 - c
f = f.monic()
roots = f.small_roots(X = 2^130,beta = 1)

print(roots)
#2E3N0Fjay4ifQ==

flag = base64.b64decode(b'VFNDVEYtSnsiclNhXzFzX2MwbXBMZXhfQnVUX0V6X3QwX2E3N0Fjay4ifQ==')
#TSCTF-J{"rSa_1s_c0mpLex_BuT_Ez_t0_a77Ack."}

ezNumberTheory

数论题说一说。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
from Crypto.Util.number import *
from secret import flag
from gmpy2 import *

len_flag = len(flag)
part_len = len_flag // 3

p = getPrime(512)
q = getPrime(512)
n = p * q
e = 65537
gift = pow(p+q,q,n)-p
m = bytes_to_long(flag[:part_len])
c = pow(m,e,n)
print("n =",n)
print("gift =",gift)
print("c =",c)
'''
n = 153749014523272882821671256288576182883718734206948338123440154330232438242352336326118817670175226476534419932398245087292627065992859219251558541981607900566708988825176882241536176428735420764037541259367530815704062276822697487906043999849153755370263421198613012659150765667474910110820544552092107031781
gift = 76218149244790410743569002423226144020409783424589996364309157429636313386270394325935494179180434848562020007440982517518325492418962399435213235272019771298535452987091692532725153721656317290106122504427984096181862152616628997041852783959323592498903124919040540241487104709669308107880042302524373888077
c = 46558926426389199704619860270058438799459155807709114710099109767026527431762127212078246374751784253888010671466257603403362846003452574724946328999962166843277258945336648937599901438703087848711983624581691213172327778561524496310162493835352841739939581338334972221480380062931473554118130953244351923526
'''

p = getPrime(512)
q = getPrime(512)
n = p * q
e = 65537
m = bytes_to_long(flag[part_len:2*part_len])
gift = pow(n-1,m,n**2)
c = pow(m,e,n)
print("n =",n)
print("gift =",gift)
print("c =",c)
'''
n = 101825028937892274755066568298675753051915211984336844010001051946487425488926444636462308770518438066690807207349397829434761111870976777194195377994066094978667372161712559828354279213717904934626695765400184018995342438568172381388749973725572499090794995578069624189552411881722996041605959223833931977161
gift = 10368336518202599155478611962986419931032852827247241544520944151147424100095888793813818133261771295138537638975002709013348196763698154979511238402220870231916534915445557931918512473116396709289462544729254616655147690181935999744990349056920271954901882532521970967307761055252723712876050094383313331140406445004997917905258680326374893836686879404331037481540004243801858344196072242572121743245711481444665694028492376994909442739868671793792049626000877294534619734785195159330183197692177383792865340479971388526007871832995878259364333594949083550807440342049213394072558604884076160696389453987350453566282
c = 6206002756473719752481539026703107851866702754011241324450943403363532188346664095512595594879972008741307201868011790850666619709952602312346601585431717191460826191100496612662950423560204126590072745286069584415447406165328489464592884522745095517397118876988652114937810284710552486235169949976593170616
'''

p = getPrime(512)
q = next_prime(p)
r = getPrime(512)
n = p * q
e = 65537
m = bytes_to_long(flag[2*part_len:])
gift = (pow(1+m*n,1,n**2)*pow(r,n,n**2))%(n**2)
print("n =",n)
print("gift =",gift)
print("p =",p)
print("q =",q)
'''
n = 120085278656547434097495160698983440086977117014813250068332400723955573086081539793659925690983763612644098938270646361630753175121916904514302168476109276991065963359696653413330575343172587757112308794397643577457876878076258704713342584783867357600427211623403743168388707834963362860793081706620920977197
gift = 755365096368274234067764643236574524026724653923904235465391689910808113641191521577417355583242717443863451427293486428108305560959934240539916731737071269870765365812729624798503913486014927177398814766178335408644263304959990001131184599054858122656321624816269434361664736002888774514548687701448375859895656340630928111228145226768972365422917506757004452665088879334351527814068349598913876771933729841797767944898598495453091334481416909244894797229851139025287531257727280929467263018600829848751441007477417666581057493947789435287529403836954674188989033519154270698877075630430517874818318137411379414838
'''

part1

$gift+p = (p+q)^q \text{(mod n)}$

$gift+p = p^q+q^q \text{(mod q)}$

$gift+p = p^p \text{(mod q)}$

根据费马小定理我们知道

$p = p^p \text{(mod q)}$

$gift + p = p \text{(modq)}$

$gift = kq$

$q = gcd(gift,n)$

得q易解

part2

$gift = (n-1)^m\text{ mod(n*n)}$

$gift = (-1)^m\text{ mod(n)}$

代入发现

$gift = 1\text{ mod(n)}$

n为奇数则m为偶数

$gift = -mn+1\text{ mod(n*n)}$

显然-mn+1为负数 而gift为正数，二者显然差一个n^2

所以$m = \frac{n^2-gift+1}{n}$

part3

比较难的CRT 第二题考到这个程度确实超模了 给大家道歉

$gift = (1+mn)(r^n)\text{ mod(nn)}$

先余n

$gift = (r^n)\text{ mod(n)}$

显然不能用费马小定理

尝试模p q

$gift = (r^{pq})\text{ mod(p)}$

$gift = (r^{pq})\text{ mod(q)}$

似乎可以做了

不妨设$d_1 = q^{-1}\text{ mod( p-1)}$

$d_2 = p^{-1}\text{ mod( q-1)}$

此时$gift^{d_1} = (r^{pqd_1}) = (r^{p(k(p-1)+1)}) = r\text{ mod(p)}$

$gift^{d_2} = (r^{pqd_2}) = (r^{q(k(q-1)+1)}) = r\text{ mod(q)}$

接下来就是CRT了 不多说

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
from Crypto.Util.number import *
n = 153749014523272882821671256288576182883718734206948338123440154330232438242352336326118817670175226476534419932398245087292627065992859219251558541981607900566708988825176882241536176428735420764037541259367530815704062276822697487906043999849153755370263421198613012659150765667474910110820544552092107031781
gift = 76218149244790410743569002423226144020409783424589996364309157429636313386270394325935494179180434848562020007440982517518325492418962399435213235272019771298535452987091692532725153721656317290106122504427984096181862152616628997041852783959323592498903124919040540241487104709669308107880042302524373888077
c = 46558926426389199704619860270058438799459155807709114710099109767026527431762127212078246374751784253888010671466257603403362846003452574724946328999962166843277258945336648937599901438703087848711983624581691213172327778561524496310162493835352841739939581338334972221480380062931473554118130953244351923526
q = GCD(gift,n)
p = n//q
phi = (p-1)*(q-1)
d = inverse(65537,phi)
m = pow(c,d,n)
m1 = long_to_bytes(m)

n = 101825028937892274755066568298675753051915211984336844010001051946487425488926444636462308770518438066690807207349397829434761111870976777194195377994066094978667372161712559828354279213717904934626695765400184018995342438568172381388749973725572499090794995578069624189552411881722996041605959223833931977161
gift = 10368336518202599155478611962986419931032852827247241544520944151147424100095888793813818133261771295138537638975002709013348196763698154979511238402220870231916534915445557931918512473116396709289462544729254616655147690181935999744990349056920271954901882532521970967307761055252723712876050094383313331140406445004997917905258680326374893836686879404331037481540004243801858344196072242572121743245711481444665694028492376994909442739868671793792049626000877294534619734785195159330183197692177383792865340479971388526007871832995878259364333594949083550807440342049213394072558604884076160696389453987350453566282
c = 6206002756473719752481539026703107851866702754011241324450943403363532188346664095512595594879972008741307201868011790850666619709952602312346601585431717191460826191100496612662950423560204126590072745286069584415447406165328489464592884522745095517397118876988652114937810284710552486235169949976593170616
m = (n**2-gift+1)//n
m2 = (long_to_bytes(m))

from functools import reduce
from Crypto.Util.number import *

import sys
n = 120085278656547434097495160698983440086977117014813250068332400723955573086081539793659925690983763612644098938270646361630753175121916904514302168476109276991065963359696653413330575343172587757112308794397643577457876878076258704713342584783867357600427211623403743168388707834963362860793081706620920977197
gift = 755365096368274234067764643236574524026724653923904235465391689910808113641191521577417355583242717443863451427293486428108305560959934240539916731737071269870765365812729624798503913486014927177398814766178335408644263304959990001131184599054858122656321624816269434361664736002888774514548687701448375859895656340630928111228145226768972365422917506757004452665088879334351527814068349598913876771933729841797767944898598495453091334481416909244894797229851139025287531257727280929467263018600829848751441007477417666581057493947789435287529403836954674188989033519154270698877075630430517874818318137411379414838
p = 10958342879128551619874835419448048277580939097878816484360833645482922440402046497462064248113450404198411413413202604271893981525662958975161222777207829
q = 10958342879128551619874835419448048277580939097878816484360833645482922440402046497462064248113450404198411413413202604271893981525662958975161222777207993
rn = gift % n

x1 = rn % p
d1 = inverse(q, p-1)
r1 = pow(x1, d1, p)

x2 = rn % q
d2 = inverse(p, q-1)
r2 = pow(x2, d2, q)


def CRT(m, a):
    Num = len(m)
    M = reduce(lambda x, y: x*y, m)
    Mi = [M//i for i in m]
    t = [inverse(Mi[i], m[i]) for i in range(Num)]
    x = 0
    for i in range(Num):
        x += a[i]*t[i]*Mi[i]
    return x % M


r = CRT([p, q], [r1, r2])

R = pow(r, n, n*n)
print(r)
R_inv = inverse(R, n*n)
mn = (gift*R_inv) % (n*n)
m = (mn-1)//n
m3 = long_to_bytes(m)

print(m1+m2+m3)

两道更比七道强！

ezPwntools

此题十分简单，会pwntools就会做

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import random
from Crypto.Util.number import *
from typing import Callable
from pwn import *
with open("flag.txt", "r") as f:
    flag = f.read().strip()

length = 128

class LCG:
    def __init__(self, length=128):
        self.length = length
        self.setparam()

    def setparam(self):
        self.m = getPrime(length+1)
        self.a = getPrime(length)
        self.b = getPrime(length)
        self.seed = random.randint(0, self.m - 1)
        self.begin = self.seed

    def generate(self):
        for i in range(10):
            self.seed = (self.a * self.seed + self.b) % self.m
        seed_list = []
        for i in range(5):
            self.seed = (self.a * self.seed + self.b) % self.m
            seed_list.append(self.seed)
        return seed_list

    def __call__(self):
        return self.begin

def challenge(input:Callable[[str],None], print:Callable[[str],None]):
    print("Welcome to TSCTF-J! If you can recover the seed, you will get the flag!")
    for i in range(512):
        lcg = LCG()
        print("Here is your gift:{}".format(lcg.generate()))
        i = input(f"Give me the seed: ")
        if int(i) != lcg():
            print(f"Oh, you are wrong!")
            return
    print(f"Congurations!{flag}")

我们发现给定五个更新完的seed，显然这里可以解同余方程把参数爆出来，但是由于要交互512次，所以这里肯定会存在几次得到的参数有小因子的情况，只需要再写一个除小因子的脚本即可。

$x_5-x_4 = a(x_4-x_3)\text{ mod(m)}$

$x_4-x_3 = a(x_3-x_2)\text{ mod(m)}$

交叉相乘把a消掉

$(x_4-x_3)^2 = (x_5-x_4)(x_3-x_2)\text{ mod(m)}$

然后不难发现

$m | (x_4-x_3)^2 - (x_5-x_4)(x_3-x_2)$

再来一个x4321的，求gcd再消掉小因子

得到m，ab都容易得到

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from Crypto.Util.number import *
from pwn import *
import ast
from tqdm import trange
def remove_small_primes(m):
    small_primes = [
        2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97,
        101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193,
        197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307,
        311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421,
        431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547,
        557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659,
        661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797,
        809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929,
        937, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021
    ]
    for prime in small_primes:
        while m % prime == 0:
            m //= prime
    return m

io = remote('challenges.hazmat.buptmerak.cn', 21764)
for i in trange(512):
    io.recvuntil(b'Here is your gift:')
    c = io.recvuntil(b']\n')
    decoded_str = c.decode('utf-8')
    x = ast.literal_eval(decoded_str)
    m = remove_small_primes(GCD((x[3]-x[2])*(x[1]-x[0])-(x[2]-x[1])*(x[2]-x[1]), (x[4]-x[3])*(x[2]-x[1])-(x[3]-x[2])*(x[3]-x[2])))
    assert(isPrime(m))
    a = ((x[2]-x[1])*inverse((x[1]-x[0]), m)) % m
    assert(isPrime(a))
    b = (x[1] - a*x[0]) % m
    assert(isPrime(b))
    seed = x[0]
    for i in range(11):
        seed = ((seed-b)*inverse(a, m)) % m
    io.sendline(str(seed))
print(io.recvline())

ezECC

为什么这题那么烂呢，因为这题是我去年出的

当时是给冬季招新用的，结果当时一个人没做出来，想着今年给复用了。

（小故事里也提到了 冬日的战斗）

其实也是为了奖励是不是真的有复盘冬季招新的人

确实挺烂的，早知道高手这么多，我就再加个曲线映射了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#sage
from Crypto.Util.number import *
from sage.all import *
msg = b'???'
flag = b'TSCTF-J{'+msg+b'}'
m = bytes_to_long(flag)
(p,a,b) = (getPrime(len(bin(bytes_to_long(flag)))) for i in range(3))
E = EllipticCurve(GF(p),[a,b])
for i in range(4):
    print(E.random_point())
e = 114514
K = E.lift_x(m+1)
eK = e*K
print(f"eK={eK}")
'''
(121542556343240612458886464797113519174471159973947349739843570016310276547868092596053087152046638137671892191449161589255393370014868931365353180578227117593735, 98840327394835055943257602264613388284774639725847294267402852043945104193135363216749971927532657727021952911622427228151863672295675502233797082353097959401869)
(99873546068894326234875062311058443230105529641172112880280159410919160848811689840010700811925066814781044568587853533466146854172381759747204462070834544581290, 54021704113721739503680080012966661376438637715420865450114718929076757346120207862947548620569435334895396324086781218017455445315421875871714429627637052871264)
(157617948261622464254152314994703598559915540865514420750304511730242939622181332932412360735409968696715108030369878546783001121709970056186086411214753185288604, 172554749510163658517336910991986476106096485848063383199885085041705448141288872247307505628175707155625972718684398442883637022240936050198926361252214588735919 )
(35601692031837010013294196210817440996871532774395053520652383520080490377765688796593595849840043210266473831404618732851470643297944496494254634489110294026906, 83109137089012676168973029782730032714034653700896174331183408691033951856596721848482516578501834370646437639802694578133409539742068584938899820955422945845189 )
eK=(148943471114336569351357302344843611917995236697008317506292328720097140911033713257363114040728547610446354966023690433690295644571622343830380563979394775174929, 5570936030363753742907439216925560949272269404612411400083981446597152991432704283038752432067099389895408182978262946903003923985122728700021027170168725851130 )
'''

给定域 $GF(p)$，椭圆曲线 $E_p: y^2 = x^3 + ax + b$ 上任意 $4$ 点 $A_1,A_2,A_3,A_4$，与 $e$ 倍基点 $K(m+1, y_{lift_x})$，$eK$ 的坐标，求 $m$。

对于点 $A_i(x_i, y_i)$ 有

$$y_i^2 \equiv x_i^3 + ax_i + b (\text{mod } p)$$

一样是先消去 $b$，用 $a$ 联立两个方程得到 $p$，然后解出 $a, b$。

利用 sage 自带的求椭圆曲线阶的函数 E.order()，求得阶为 $P$，这个题就转化为了：

$K$ 为椭圆曲线 $E_p$ 上一点，已知 $eK$，$e$，求 $K$。

求出 $e$ 关于阶 $P$ 的逆元即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from Crypto.Util.number import *
from sage.all import *
list=[]
(x1,y1)=(121542556343240612458886464797113519174471159973947349739843570016310276547868092596053087152046638137671892191449161589255393370014868931365353180578227117593735, 98840327394835055943257602264613388284774639725847294267402852043945104193135363216749971927532657727021952911622427228151863672295675502233797082353097959401869)
(x2,y2)=(99873546068894326234875062311058443230105529641172112880280159410919160848811689840010700811925066814781044568587853533466146854172381759747204462070834544581290, 54021704113721739503680080012966661376438637715420865450114718929076757346120207862947548620569435334895396324086781218017455445315421875871714429627637052871264)
(x3,y3)=(157617948261622464254152314994703598559915540865514420750304511730242939622181332932412360735409968696715108030369878546783001121709970056186086411214753185288604, 172554749510163658517336910991986476106096485848063383199885085041705448141288872247307505628175707155625972718684398442883637022240936050198926361252214588735919 )
(x4,y4)=(35601692031837010013294196210817440996871532774395053520652383520080490377765688796593595849840043210266473831404618732851470643297944496494254634489110294026906, 83109137089012676168973029782730032714034653700896174331183408691033951856596721848482516578501834370646437639802694578133409539742068584938899820955422945845189 )
eK=(148943471114336569351357302344843611917995236697008317506292328720097140911033713257363114040728547610446354966023690433690295644571622343830380563979394775174929, 5570936030363753742907439216925560949272269404612411400083981446597152991432704283038752432067099389895408182978262946903003923985122728700021027170168725851130 )
t1 = (y2**2-y1**2-x2**3+x1**3)
t2 = (y3**2-y2**2-x3**3+x2**3)
t3 = (y4**2-y3**2-x4**3+x3**3)
k1p = t1*(x3-x2) - t2*(x2-x1)
k2p = t2*(x4-x3) - t3*(x3-x2)
k3p = t1*(x4-x3) - t3*(x2-x1)
p = GCD(k1p,k2p)
for i in range(2,1000):
    while(p % i == 0):
        p //= i
a = inverse(x2-x1,p)*t1 % p
b = (y1**2-x1**3-a*x1) % p
print(a,b,p)


E = EllipticCurve(GF(p),[a,b])
#print(E(eK[0],eK[1]).order())
order = 137158282955653987884883849194331997445549656524852531414041071058772175899425275190380665644090833671963444295215087328717770758449529501165286488193579249001703
e = 114514
t = inverse(e,order)
eK=E.lift_x(148943471114336569351357302344843611917995236697008317506292328720097140911033713257363114040728547610446354966023690433690295644571622343830380563979394775174929)
print(long_to_bytes(int((eK*int(t))[0]-1)))


ezFakekey

这题应该能算是我的得意之作吧，有种pwn密码的美感，灵感来源于2023熵密杯初始谜题。

来源于CBC翻转，但做了一点改进。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
from Crypto.Cipher import AES
from Crypto.Random import get_random_bytes
from typing import Callable
with open("flag.txt", "r") as f:
    flag = f.read().strip()

def pad(data):
    pad_len = 16 - len(data) % 16
    return data + bytes([pad_len] * pad_len)

def unpad(data):
    pad_len = data[-1]
    return data[:-pad_len]

def generate_key():
    return get_random_bytes(32) 

def generate_iv():
    return get_random_bytes(16) 

def encrypt(message, key, iv):
    assert len(key) == 32
    assert len(iv) == 16
    cipher = AES.new(key, AES.MODE_CBC, iv)
    ciphertext = cipher.encrypt(pad(message))
    return ciphertext

def decrypt(ciphertext, key, iv):
    assert len(key) == 32
    assert len(iv) == 16
    cipher = AES.new(key, AES.MODE_CBC, iv)
    plaintext = unpad(cipher.decrypt(ciphertext))
    return plaintext

def challenge(input:Callable[[str],None], print:Callable[[str],None]):
    print("Welcome to TSCTF-J! If you are Administrator, I will give you a flag!")
    key = generate_key()
    iv = generate_iv()
    while True:
        print('[E]ncrypt the message')
        print('[D]ecrypt the message')
        print('[G]et the flag')
        print('[Q]uit')
        option = input('> ').upper()
        if option == 'E':
            input_message = input('Plz input your message: ')
            m = input_message.encode()
            if b'Administrator' in m:
                print('Permission denied!')
                return
            ciphertext = encrypt(m, key, iv)
            print(f'Your ciphertext: {ciphertext.hex()}')
        elif option == 'D':
            ciphertext = bytes.fromhex(input('Plz input the ciphertext: '))
            m = ciphertext
            plaintext = decrypt(m, key, iv)
            print(f'Your plaintext: {plaintext}')
        elif option == 'G':
            ciphertext = bytes.fromhex(input('Plz input the ciphertext: '))
            m = ciphertext
            plaintext = decrypt(m, key, iv)
            if b'Administrator' in plaintext:
                print(f'Congurations!Here is flag:{flag}')
                return
            else:
                print('Permission denied!')
        elif option == 'Q':
            return
        else:
            print('Unknown option:', option)

让我们把CBC原理搬出来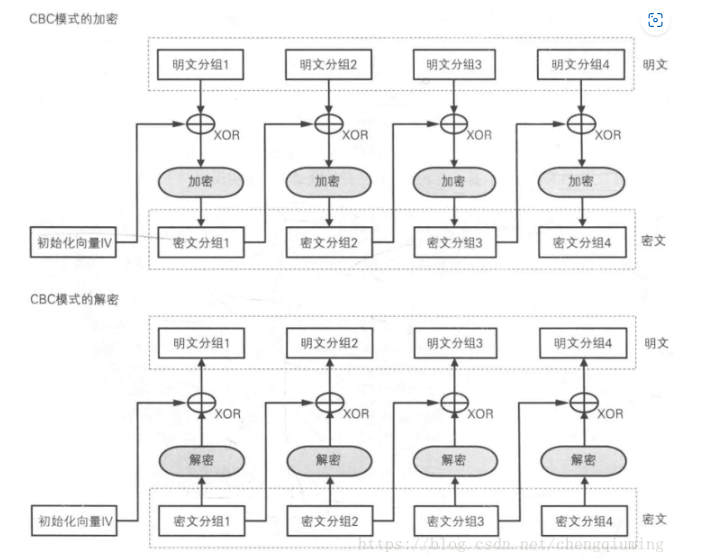image-20240924201801788.png。

我们需要伪造密文，使得解密后存在b’Administrator’字段。

观察代码容易发现iv和key都是一样的。

怎么伪造呢

我们可以在网上搜索CBC翻转攻击，会发现关键出在异或上。

假设我们加密b’a’*32 会发现密文分组二是由明文分组一和密文分组一 异或再加密得到的。

那么反过来，如果我们已经知道了密文分组二在直接经过解密的结果（还没和密文分组一异或之前）我们可以故意构造密文分组一，达到效果。

用文字说太累了，还是写点公式吧。

我们加密b’a’*32，这部分会分为为两块，设为$pad_1$,$pad_2$.

密文分组一

$cip_1 = AES(pad_1\oplus IV)$

$cip_2 = AES(pad_2\oplus cip_1)$

想要让明文分组2为Administrator

可令$payload_1 = pad_2 \oplus cip_1 \oplus b’Administrator’$

此时$cip_2$解密完就是$(pad_2\oplus cip_1)$

和payload1异或就是b’Administrator’

看来下次得多出点这种纯密码题了，老出数学大家都思维惯性了^^.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from pwn import *
import itertools
def pad(data):
    pad_len = 16 - len(data) % 16
    return data + bytes([pad_len] * pad_len)

def xor_bytes(a, b):
    return bytes(itertools.starmap(operator.xor, zip(a, b)))

context.log_level = 'debug'
io = remote('challenges.hazmat.buptmerak.cn',20185)
q=pow(2,555)-19
io.recvuntil('> ')
io.sendline('e')
io.sendline(b'a'*32)
cipher = io.recvline()[41:-1]
cipher1 = bytes.fromhex(cipher.decode())
payload = xor_bytes(xor_bytes(cipher1[:16], b'a'*16),pad(b'Administrator')) + cipher1[16:]
io.recvuntil('> ')
io.sendline('g')
io.sendline(payload.hex())
io.recvline()

真的很像pwn题

后记

哎 这么快一年就过去了，追上前浪还很远，后浪却已在眼前，今年出的这么难，还是有学弟能做完（虽然有非预期），确实很厉害啊，感觉已经到我今年二月做hgame的水平了。

去年的我一个非预期，三个简单题，居然还能拿第二，有点狗屎运了现在看来。

我也得多学点东西，不能被超过才是。

#CTF #Crypto
2024-TSCTF-J-partWP-crypto
https://py-thok.github.io/2024/09/24/2024-TSCTF-J-partWP-crypto/
作者
PYthok-Ptk
发布于
2024年9月24日
许可协议