2024-熵密杯-wp-Crypto

2024-熵密杯-wp-crypto

很荣幸和学长一起去银川打了这场比赛，本人主要负责前几题，主要还是靠mix学长的审计和bartleby学长的超绝推导，最后拿下二等奖第七名。

虽然最后差一点ak，但是当时就算做出来最后一题因为没血也只能拿第六，所以也没什么所谓了

也见到了我非常喜欢的糖醋小鸡块师傅！

银川连着下了四天的雨，但是羊肉很好吃。

当时去坐飞机甚至还满座升舱了，运气真好。

简单写写。

规则

当时忘记把比赛规则带出来了，印象里是三道初始谜题，然后做出来任意一道可以进入第二轮，第二轮有两条路径，flag1->flag2,flag3->flag4，必须把flag2和flag4都做出来才能到最终环节，最终环节就是一个签名的伪造，当时就是卡在最终环节一直没签上。

初始谜题1

其实说实话，熵密杯的题和一般的ctf题目非常不一样，比如我还没有见到用sympy写题面的题目。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
from sympy import Mod, Integer
from sympy.core.numbers import mod_inverse

from Crypto.Util.number import long_to_bytes
# 模数
N_HEX = "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123"
MODULUS = Integer(int(N_HEX, 16))
MSG_PREFIX = "CryptoCup message:"


# 加密函数
def encrypt_message(message, key):
    # 添加前缀
    message_with_prefix = MSG_PREFIX + message
    message_bytes = message_with_prefix.encode('utf-8')
    message_len = len(message_bytes)
    num_blocks = (message_len + 15) // 16
    blocks = [message_bytes[i * 16:(i + 1) * 16] for i in range(num_blocks)]

    # 进行0填充
    blocks[-1] = blocks[-1].ljust(16, b'\x00')

    encrypted_blocks = []

    k = key

    # 加密每个分组
    for block in blocks:
        block_int = int.from_bytes(block, byteorder='big')
        print("block_int ",block_int)
        encrypted_block_int = Mod(block_int * k, MODULUS)
        encrypted_blocks.append(encrypted_block_int)
        k += 1  # 密钥自增1

    print(encrypted_blocks)
    

    encrypted_list = []
    # 将加密后的分组连接成最终的密文
    encrypted_list.append(
        [int(block_int).to_bytes(32, byteorder='big') for block_int in encrypted_blocks]
    )

    return encrypted_list


# 解密函数
def decrypt_message(encrypted_message, key):
    num_blocks = len(encrypted_message) // 32
    blocks = [encrypted_message[i * 32:(i + 1) * 32] for i in range(num_blocks)]

    decrypted_blocks = []

    k = key

    # 解密每个分组
    for block in blocks:
        block_int = int.from_bytes(block, byteorder='big')
        key_inv = mod_inverse(k, MODULUS)
        decrypted_block_int = Mod(block_int * key_inv, MODULUS)
        decrypted_blocks.append(decrypted_block_int)
        k += 1  # 密钥自增1

    # 将解密后的分组连接成最终的明文
    decrypted_message = b''.join(
        long_to_bytes(int(block_int)) for block_int in decrypted_blocks
    )

    # 去除前缀
    if decrypted_message.startswith(MSG_PREFIX.encode('utf-8')):
        decrypted_message = decrypted_message[len(MSG_PREFIX):]

    return decrypted_message


# 测试
initial_key = Integer(0x123456789ABCDEF0123456789ABCDEF0123456789ABCDEF0123456789ABCDEF0)
message = "Hello, this is a test message.asasfaefaasasaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
#print("Original Message:", message)

# 加密
encrypted_message = encrypt_message(message, initial_key)
#print("Encrypted Message (hex):", encrypted_message.hex())
print(encrypted_message)
# 解密
decrypted_message = decrypt_message(encrypted_message, initial_key)
#print("Decrypted Message:", decrypted_message)


ciphertext = long_to_bytes(0x5cae321c794c785089ccebc7fcdf834937857ee003b8e84a61392ddc774cfc16a7e0ca4268d31c0db6f993431df2e180e4ede0d2f6e51cd503c4dfc0c059a09610478208399e45679cad7651c1dd1060aad3137dc0d464ac67e4b776266895a5f4d760d64ed46b7e2302793ba366fb4d3f97abfa9f88b9a9329902764d555cc1)
print(encrypt_message('',initial_key))
print(encrypt_message('0',initial_key))


当时看的时候没什么感觉，感觉可能是格？后来队友提醒说这个部分明文是已知的，这才恍然大悟，可以直接解出key，然后后面就是简单的求逆的过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#flag1
from sympy import Mod, Integer
from sympy.core.numbers import mod_inverse

from Crypto.Util.number import *
cipher = 0x5cae321c794c785089ccebc7fcdf834937857ee003b8e84a61392ddc774cfc16a7e0ca4268d31c0db6f993431df2e180e4ede0d2f6e51cd503c4dfc0c059a09610478208399e45679cad7651c1dd1060aad3137dc0d464ac67e4b776266895a5f4d760d64ed46b7e2302793ba366fb4d3f97abfa9f88b9a9329902764d555cc1
N_HEX = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123

initial_key = Integer(0x123456789ABCDEF0123456789ABCDEF0123456789ABCDEF0123456789ABCDEF0)
a = 89652660640613347754090896429354803559
b = 37681243689413481885669644652084398160214259040017619160297065760370037876043
print((b*inverse(a,N_HEX))%N_HEX)
print(int(initial_key))


given_cipher = 0x5cae321c794c785089ccebc7fcdf834937857ee003b8e84a61392ddc774cfc16a7e0ca4268d31c0db6f993431df2e180e4ede0d2f6e51cd503c4dfc0c059a09610478208399e45679cad7651c1dd1060aad3137dc0d464ac67e4b776266895a5f4d760d64ed46b7e2302793ba366fb4d3f97abfa9f88b9a9329902764d555cc1
cipher_byte = long_to_bytes(given_cipher)
num_blocks = len(cipher_byte) // 32
blocks = [cipher_byte[i * 32:(i + 1) * 32] for i in range(num_blocks)]
block_int = [bytes_to_long(i) for i in blocks]
print(block_int)
a = 89652660640613347754090896429354803559
print(block_int[0]*inverse(a,N_HEX)%N_HEX)
hidekey = block_int[0]*inverse(a,N_HEX)%N_HEX

N_HEX = "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123"
MODULUS = Integer(int(N_HEX, 16))
MSG_PREFIX = "CryptoCup message:"

# 解密函数
def decrypt_message(encrypted_message, key):
    num_blocks = len(encrypted_message) // 32
    blocks = [encrypted_message[i * 32:(i + 1) * 32] for i in range(num_blocks)]

    decrypted_blocks = []

    k = key

    # 解密每个分组
    for block in blocks:
        block_int = int.from_bytes(block, byteorder='big')
        key_inv = mod_inverse(k, MODULUS)
        decrypted_block_int = Mod(block_int * key_inv, MODULUS)
        decrypted_blocks.append(decrypted_block_int)
        k += 1  # 密钥自增1

    # 将解密后的分组连接成最终的明文
    decrypted_message = b''.join(
        long_to_bytes(int(block_int)) for block_int in decrypted_blocks
    )

    # 去除前缀
    if decrypted_message.startswith(MSG_PREFIX.encode('utf-8')):
        decrypted_message = decrypted_message[len(MSG_PREFIX):]

    return decrypted_message

print(decrypt_message(cipher_byte,hidekey))

简单解密完之后是一串字符，然后用他给的client端提交即可。

1
2
3
4
5
验证通过
flag{8FSPTfuRIdOIxpoWRrXEBph93le6GjEv}
gitea账号：giteauser2024
gitea口令：S(*HD^WY63y89TY71
提示：gitea账号和口令用于登录第二环节的gitea服务器，请注意保存！

初始谜题2

sm3长度扩展攻击，包括md类的所有散列函数都会有这种问题。

其实之前在数信杯做过这道题了，但是之前没出，保存的脚本在比赛的时候死活用不上，最后一个人熬到12点硬看源码做出来了，当时10多人出，没拿到血还是很可惜。

简单分析一下源码吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def sm3_hash(msg):
    # print(msg)
    len1 = len(msg)
    reserve1 = len1 % 64
    msg.append(0x80)
    reserve1 = reserve1 + 1
    # 56-64, add 64 byte
    range_end = 56
    if reserve1 > range_end:
        range_end = range_end + 64

    for i in range(reserve1, range_end):
        msg.append(0x00)

    bit_length = (len1) * 8
    bit_length_str = [bit_length % 0x100]
    for i in range(7):
        bit_length = int(bit_length / 0x100)
        bit_length_str.append(bit_length % 0x100)
    for i in range(8):
        msg.append(bit_length_str[7-i])

    group_count = round(len(msg) / 64)

    B = []
    for i in range(0, group_count):
        B.append(msg[i*64:(i+1)*64])

    V = []
    V.append(IV)
    for i in range(0, group_count):
        V.append(sm3_cf(V[i], B[i]))

    y = V[i+1]
    result = ""
    for i in y:
        result = '%s%08x' % (result, i)
    return result

大概就是说如果明文大于等于56字节就会分块，但是他的这一次的hash值是由上一块的hash值和这一块明文共同决定的。

$${hash}i = CF({hash}{i-1},{plain}_{i-1})$$

所以说如果上一块明文和上一块的hash都是已知的，那么我们可以扩展他的长度，来推断出下一块的hash以及最终的$sm3(plain)$。

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import binascii
from gmssl import sm3


# 读取HMAC key文件
def read_hmac_key(file_path):
    with open(file_path, 'rb') as f:
        hmac_key = f.read().strip()
    return hmac_key


# 生成token
def generate_token(hmac_key, counter):
    # 如果HMAC_KEY长度不足32字节，则在末尾补0，超过64字节则截断
    if len(hmac_key) < 32:
        hmac_key = hmac_key.ljust(32, b'\x00')
    elif len(hmac_key) > 32:
        hmac_key = hmac_key[:32]

    # 将计数器转换为字节表示
    counter_bytes = counter.to_bytes((counter.bit_length() + 7) // 8, 'big')
    # print("counter_bytes:", binascii.hexlify(counter_bytes))

    tobe_hashed = bytearray(hmac_key + counter_bytes)

    # print("tobe_hashed:", binascii.hexlify(tobe_hashed))

    # 使用SM3算法计算哈希值
    sm3_hash = sm3.sm3_hash(tobe_hashed)

    # 将SM3的哈希值转换为十六进制字符串作为token
    token = sm3_hash

    return token


current_counter = 0


def verify_token(hmac_key, counter, token):
    # 生成token
    generated_token = generate_token(hmac_key, counter)
    global current_counter
    # 比较生成的token和输入的token是否相同
    if generated_token == token:
        if counter & 0xFFFFFFFF > current_counter:
            current_counter = counter & 0xFFFFFFFF
            print("current_counter: ", hex(current_counter))
            return "Success"
        else:
            return "Error: counter must be increasing"
    else:
        return "Error: token not match"


# 假设HMAC key文件路径
hmac_key_file = 'hmac_key.txt'
# 假设计数器值
counter = 0x12345678

# 读取HMAC key
hmac_key = read_hmac_key(hmac_key_file)

# 生成token
token = generate_token(hmac_key, counter)
print("Generated token:", token)
print(verify_token(hmac_key, counter, token))

在这个题目里其实有一个要求就是counter必须递增，这看起来很难其实只需要让最后的明文是\xff*8即可。

简单上个exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from gmssl import sm3
import binascii
from math import ceil
from Crypto.Util.number import *
rotl = lambda x, n:((x << n) & 0xffffffff) | ((x >> (32 - n)) & 0xffffffff)
def turn(a):
    vectors = []
    for r in range(0, len(a), 8):
        vectors.append(int(a[r:r + 8], 16))
    return (vectors)
msg = bytearray(b'testtesttesttesttesttesttesttesttest')

def xxx(a):
    result = ""
    for i in a:
        result = '%s%08x' % (result, i)
    return result

a = (sm3.sm3_hash(msg))
#hmackey+counter = 32+4
given_hash = "e965992687d956f6c38748bc7334a98a8e65530ace4742ea88ecdebd65fe3cc9"

counter = 0x79209583
my_B = bytearray(b'\xff\xff\xff\xff\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x02 ')


print("!!!!",xxx(sm3.sm3_cf(turn(given_hash),my_B)))
#5bfa469312fc46e45fb27a492b6394b2d830aa13d29384edff66418148914c2e
print((sm3.sm3_hash(bytearray(b'testtesttesttesttesttesttesttesttest\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x01 \xff\xff\xff\xff'))))
print(hex(bytes_to_long(b'testtesttesttesttesttesttesttest\x75\xa5\xcd\xe4\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x01 \xff\xff\xff\xff')))

初始谜题3

这题就是一个lwe，但是是学长做的，后来看了发现e只有2**16，所以是完全可以爆破的。

所以把e爆破出来直接解方程就出了，当时做出来的人也很多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import sympy as sp
import random

# 设置参数
n = 16  # 向量长度
q = 251  # 模数

# 生成随机噪声向量e
e = sp.Matrix(sp.randMatrix(n, 1, min=0, max=1))  # 噪声向量

# 生成随机n维私钥向量s和n*n矩阵A
s = sp.Matrix(sp.randMatrix(n, 1, min=0, max=q - 1))  # 私钥向量
Temp = sp.Matrix(sp.randMatrix(n, n, min=0, max=q - 1))  # 中间变量矩阵Temp
A = Temp.inv_mod(q)  # 计算矩阵Temp在模 q 下的逆矩阵作为A

# 计算n维公钥向量b
b = (A * s + e) % q  # 公钥向量b = A * s + e


# 加密函数
def encrypt(message, A, b):
    m_bin = bin(message)[2:].zfill(n)  # 将消息转换为16比特的二进制字符串
    m = sp.Matrix([int(bit) for bit in m_bin])  # 转换为SymPy矩阵
    x = sp.Matrix(sp.randMatrix(n, n, min=0, max=q // (n * 4)))  # 随机产生一个n*n的矩阵x
    e1 = sp.Matrix(sp.randMatrix(n, 1, min=0, max=1))  # 随机产生一个n维噪声向量e
    c1 = (x * A) % q  # 密文部分c1 =   x * A
    c2 = (x * b + e1 + m * (q // 2)) % q  # 密文部分c2 = x * b + e1 + m * q/2
    return c1, c2


# 解密函数
def decrypt(c1, c2, s):
    m_dec = (c2 - c1 * s) % q
    m_rec = m_dec.applyfunc(lambda x: round(2 * x / q) % 2)  # 还原消息
    m_bin = ''.join([str(bit) for bit in m_rec])  # 将SymPy矩阵转换为二进制字符串
    m_rec_int = int(m_bin, 2)  # 将二进制字符串转换为整数
    return m_rec_int


# 测试加解密
message = random.randint(0, 2 ** n - 1)  # 要加密的消息，随机生成一个16比特整数
c1, c2 = encrypt(message, A, b)  # 加密

print("原始消息: ", message)
print("公钥A=sp.", A)
print("公钥b=sp.", b)
print("密文c1=sp.", c1)
print("密文c2=sp.", c2)

decrypted_message = decrypt(c1, c2, s)
print("解密后的消息: ", decrypted_message)  # 输出解密后的消息
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
q = 251
G = GF(q)
A = Matrix(G,[[221, 127, 167, 140, 199, 232, 222, 196, 1, 246, 49, 165, 59, 97, 206, 122], [109, 186, 186, 138, 216, 115, 65, 163, 139, 166, 186, 108, 235, 26, 146, 50], [106, 74, 19, 10, 111, 88, 10, 142, 148, 74, 84, 44, 76, 125, 135, 48], [138, 24, 193, 190, 12, 181, 229, 44, 48, 246, 115, 1, 33, 8, 164, 47], [172, 68, 185, 199, 78, 133, 50, 94, 160, 100, 202, 18, 229, 129, 25, 66], [47, 244, 225, 149, 106, 126, 78, 84, 193, 24, 183, 136, 99, 64, 169, 217], [147, 33, 234, 101, 134, 29, 210, 217, 39, 246, 162, 212, 40, 37, 137, 101], [140, 214, 38, 115, 32, 247, 125, 99, 240, 126, 12, 46, 169, 232, 66, 8], [90, 127, 223, 1, 39, 24, 180, 15, 100, 114, 62, 89, 157, 68, 159, 174], [214, 213, 243, 113, 121, 48, 29, 54, 90, 236, 32, 74, 247, 87, 37, 97], [121, 189, 117, 202, 32, 77, 41, 36, 117, 23, 46, 76, 194, 141, 7, 138], [183, 241, 176, 248, 149, 56, 163, 17, 181, 40, 115, 246, 95, 70, 128, 164], [120, 49, 189, 204, 152, 29, 229, 172, 155, 140, 127, 3, 110, 34, 48, 49], [101, 156, 234, 128, 219, 201, 225, 43, 22, 217, 247, 187, 13, 96, 124, 6], [129, 105, 45, 14, 168, 214, 33, 183, 37, 243, 11, 3, 194, 17, 53, 74], [210, 9, 16, 165, 90, 142, 189, 82, 39, 159, 183, 164, 82, 235, 239, 141]])

b = Matrix(G,[[208], [185], [45], [175], [138], [113], [217], [206], [205], [15], [184], [135], [43], [95], [234], [170]])

c1 = Matrix(G,[[127, 90, 38, 137, 249, 34, 205, 116, 219, 131, 139, 237, 223, 202, 184, 163], [29, 44, 107, 78, 248, 79, 139, 122, 127, 165, 188, 113, 43, 72, 198, 105], [99, 88, 7, 129, 237, 55, 239, 157, 37, 189, 188, 207, 228, 166, 80, 83], [25, 223, 56, 35, 62, 3, 99, 239, 96, 15, 239, 132, 16, 234, 168, 143], [71, 44, 104, 130, 240, 90, 94, 136, 59, 4, 170, 102, 100, 70, 206, 11], [5, 58, 220, 136, 151, 101, 183, 245, 35, 197, 143, 177, 93, 177, 4, 29], [246, 12, 215, 117, 173, 222, 55, 117, 183, 187, 124, 40, 69, 192, 220, 185], [197, 144, 242, 97, 182, 59, 129, 64, 86, 52, 79, 163, 44, 159, 61, 83], [170, 202, 30, 234, 196, 193, 205, 198, 245, 49, 135, 93, 46, 45, 12, 162], [228, 156, 36, 84, 79, 184, 1, 50, 197, 137, 171, 116, 131, 64, 136, 49], [63, 182, 170, 164, 100, 80, 116, 95, 140, 55, 187, 43, 152, 141, 12, 232], [17, 92, 142, 86, 35, 222, 59, 177, 76, 64, 206, 173, 160, 125, 182, 112], [247, 144, 243, 147, 145, 100, 11, 121, 188, 243, 25, 236, 74, 236, 148, 66], [218, 123, 213, 237, 194, 202, 13, 31, 66, 241, 144, 86, 155, 74, 174, 112], [19, 7, 55, 106, 53, 49, 35, 106, 201, 220, 89, 235, 148, 72, 170, 88], [186, 76, 86, 89, 54, 203, 186, 142, 8, 86, 174, 115, 133, 227, 104, 107]])

c2 = Matrix(G,[[235], [9], [224], [158], [103], [151], [7], [124], [159], [100], [23], [199], [206], [125], [235], [10]])

# from sage.all import *
# const = 2**8
# M1 = block_matrix([[A.T],[b.T],[identity_matrix(16)*q]]) * const
# M2 = Matrix(17+16, 17)
# for _ in range(16):
#     M2[_,_] = 1
# M2[16,16] = const
# M = block_matrix([M1,M2],ncols=2)
# ML = M.LLL()


def decrypt(c1, c2, s):
    m_dec = (c2 - c1 * s).T
    m_rec = [round(2 * int(_) / q) % 2 for _ in m_dec[0]]
    m_bin = ''.join([str(bit) for bit in m_rec])  # 将SymPy矩阵转换为二进制字符串
    m_rec_int = int(m_bin, 2)  # 将二进制字符串转换为整数
    return m_rec_int

from tqdm import trange
from Crypto.Util.number import long_to_bytes
G = GF(q)
for i in trange(2**16):
    e = Matrix(G,[int(_) for _ in bin(i)[2:].rjust(16,'0')]).T
    s = A.solve_right(b - e)
    msg = decrypt(c1,c2,s)
    if msg.bit_length() <= 16:
        print(msg)
    # flag = long_to_bytes(msg)
    # if b'flag' in flag:
    #     print(flag)

也许密码应该优先考虑爆破？有点难绷了。

flag1

这题其实和当时2023熵密杯的第二题非常相似，但是当时直接逆回来写就出了，这一次我们死活没出，最后是爆破2**32出的，后来上的hint也提示说应该多线程爆破，最后三台电脑一起跑，大概两三分钟就出了。

题目莫得了，只有exp。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
#include <stdio.h>
#include <string.h>
#include <unistd.h>
#include <stdlib.h>
#include <sys/wait.h>
#include <openssl/sha.h>

#define ROUND 16

// S-Box 16x16
unsigned char rev_sBox[] = {13, 4, 0, 5,
                            2, 12, 11, 8,
                            10, 6, 1, 9,
                            3, 15, 7, 14};

// 将十六进制字符串转换为 unsigned char 数组
void hex_to_bytes(const char *hex_str, unsigned char *bytes, size_t bytes_len)
{
    size_t hex_len = strlen(hex_str);
    if (hex_len % 2 != 0 || hex_len / 2 > bytes_len)
    {
        fprintf(stderr, "Invalid hex string length.\n");
        return;
    }

    for (size_t i = 0; i < hex_len / 2; i++)
    {
        sscanf(hex_str + 2 * i, "%2hhx", &bytes[i]);
    }
}

// 派生轮密钥
void derive_round_key(unsigned int key, unsigned char *round_key, int length)
{

    unsigned int tmp = key;
    for (int i = 0; i < length / 16; i++)
    {
        memcpy(round_key + i * 16, &tmp, 4);
        tmp++;
        memcpy(round_key + i * 16 + 4, &tmp, 4);
        tmp++;
        memcpy(round_key + i * 16 + 8, &tmp, 4);
        tmp++;
        memcpy(round_key + i * 16 + 12, &tmp, 4);
        tmp++;
    }
}

// 比特逆序
void reverseBits(unsigned char *state)
{
    unsigned char temp[16];
    for (int i = 0; i < 16; i++)
    {
        unsigned char byte = 0;
        for (int j = 0; j < 8; j++)
        {
            byte |= ((state[i] >> j) & 1) << (7 - j);
        }
        temp[15 - i] = byte;
    }
    for (int i = 0; i < 16; i++)
    {
        state[i] = temp[i];
    }
}

void rev_leftShiftBytes(unsigned char *state)
{
    unsigned char temp[4];
    for (int i = 0; i < 16; i += 4)
    {
        temp[0] = ((state[i + 2] & 0x7) << 5) | (state[i + 3] >> 3);
        temp[1] = ((state[i + 3] & 0x7) << 5) | (state[i + 0] >> 3);
        temp[2] = ((state[i + 0] & 0x7) << 5) | (state[i + 1] >> 3);
        temp[3] = ((state[i + 1] & 0x7) << 5) | (state[i + 2] >> 3);
        memcpy(state + i, temp, sizeof temp);
    }
}

void rev_sBoxTransform(unsigned char *state)
{
    for (int i = 0; i < 16; i++)
    {
        unsigned char lo = rev_sBox[state[i] & 0xF];
        unsigned char hi = rev_sBox[state[i] >> 4];
        state[i] = (hi << 4) | lo;
    }
}

void addRoundKey(unsigned char *state, unsigned char *roundKey, unsigned int round)
{
    for (int i = 0; i < 16; i++)
    {
        for (int j = 0; j < 8; j++)
        {
            state[i] ^= ((roundKey[i + round * 16] >> j) & 1) << j;
        }
    }
}

void decrypt(const unsigned char *ciphertext, unsigned int key, unsigned char *cleartext)
{
    unsigned char roundKeys[16 * ROUND] = {};

    derive_round_key(key, roundKeys, 16 * ROUND);

    unsigned char state[16];
    memcpy(state, ciphertext, sizeof state);

    for (int round = ROUND - 1; round >= 0; round--)
    {
        addRoundKey(state, roundKeys, round);
        rev_leftShiftBytes(state);
        rev_sBoxTransform(state);
        reverseBits(state);
    }

    memcpy(cleartext, state, sizeof state);
}

int main(int argc, char **argv)
{
    unsigned char ciphertext[16];
    hex_to_bytes("99F2980AAB4BE8640D8F322147CBA409", ciphertext, sizeof ciphertext);

    unsigned char cleartext[17] = {0};
    for (unsigned int key = 0x80000000; key <= 0xFFFFFFFF; key++)
    {
        if (key % 0xFFFFFF == 0)
        {
            printf("key %08X reached\n", key);
        }
        decrypt(ciphertext, key, cleartext);
        if (strncmp(cleartext, "pwd:", 4) == 0)
        {
            printf("valid cleartext found! key=%08X ct=%s", key, cleartext);
            // return 0;
        }
    }

    return 0;
}

当时不知道是不是0ops，没拿flag1就拿到flag2了，有点难绷，经典复刻了。

然后爆破就可以拿到压缩包密码，压缩包里面有第一个flag

image-20240905144307852

flag2

第二个flag还挺有意思。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
#include <stdio.h>
#include <stdlib.h>
#include <openssl/ec.h>
#include <openssl/rand.h>

#define SM2LEN 32

int error() {
    printf("Error.\n");
    return 0;
}

int error_partial_verify() {
    printf("Error partial verify.\n");
    return 0;
}

void print_flag2(const BIGNUM *d2) {
    char *hex_str = BN_bn2hex(d2);
    for (int i = 0; hex_str[i] != '\0'; i++) {
        if (hex_str[i] >= 'A' && hex_str[i] <= 'F') {
            hex_str[i] += 32;
        }
    }
    printf("flag2{%s}\n", hex_str);
}

typedef struct {
    char s2[SM2LEN * 2 + 1];
    char s3[SM2LEN * 2 + 1];
    char r[SM2LEN * 2 + 1];
    int success;
} Result;

// 协同签名服务端签名算法
Result server(char* str_e,char* str_p1x,char* str_p1y,char* str_q1x,char* str_q1y,char* str_r1,char* str_s1){
    Result res = {"", "", "", 0};

	int rv = 1;
	BIGNUM *e,*a,*b,*p,*n,*x,*y;
	BIGNUM *d2,*r1,*s1,*p1x,*p1y,*q1x,*q1y;
	BIGNUM *u1,*u2,*xprime,*yprime,*k2,*k3,*x1,*y1,*r,*s2,*s3,*s,*tmp1,*tmp2,*tmp3;
	EC_GROUP* group;
	EC_POINT *generator,*G,*P,*P1,*Q1,*TMP;

	BN_CTX* bn_ctx = BN_CTX_new();
	BN_CTX_start(bn_ctx);
	if (!bn_ctx)
		{ error(); return res; }
	e = BN_CTX_get(bn_ctx);
	a = BN_CTX_get(bn_ctx);
	b = BN_CTX_get(bn_ctx);
	p = BN_CTX_get(bn_ctx);
	n = BN_CTX_get(bn_ctx);
	d2 = BN_CTX_get(bn_ctx);
	x = BN_CTX_get(bn_ctx);
	y = BN_CTX_get(bn_ctx);
	p1x = BN_CTX_get(bn_ctx);
	p1y = BN_CTX_get(bn_ctx);
	q1x = BN_CTX_get(bn_ctx);
	q1y = BN_CTX_get(bn_ctx);
	r1 = BN_CTX_get(bn_ctx);
	s1 = BN_CTX_get(bn_ctx);
	u1 = BN_CTX_get(bn_ctx);
	u2 = BN_CTX_get(bn_ctx);
	xprime = BN_CTX_get(bn_ctx);
	yprime = BN_CTX_get(bn_ctx);
	k2 = BN_CTX_get(bn_ctx);
	k3 = BN_CTX_get(bn_ctx);
	x1 = BN_CTX_get(bn_ctx);
	y1 = BN_CTX_get(bn_ctx);
	r = BN_CTX_get(bn_ctx);
	s2 = BN_CTX_get(bn_ctx);
	s3 = BN_CTX_get(bn_ctx);
	s = BN_CTX_get(bn_ctx);
	tmp1 = BN_CTX_get(bn_ctx);
	tmp2 = BN_CTX_get(bn_ctx);
	tmp3 = BN_CTX_get(bn_ctx);

	if (
		!BN_hex2bn(&e, str_e) ||
		!BN_hex2bn(&p1x, str_p1x) ||
		!BN_hex2bn(&p1y, str_p1y) ||
		!BN_hex2bn(&q1x, str_q1x) ||
		!BN_hex2bn(&q1y, str_q1y) ||
		!BN_hex2bn(&r1, str_r1) ||
		!BN_hex2bn(&s1, str_s1) ||
		!BN_hex2bn(&a, "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC") ||
		!BN_hex2bn(&b, "28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93") ||
		!BN_hex2bn(&p, "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF") ||
		!BN_hex2bn(&n, "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123") ||
		// d2 = ds (server key)
		!BN_hex2bn(&d2, "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX") ||
		!BN_hex2bn(&x, "32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7") ||
		!BN_hex2bn(&y, "BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0") ||
		!BN_rand_range(k2,n) ||
		!BN_copy(k3, k2)
		)
		{ error(); return res; }

    // generate k2 in [1, n-1]
	while(BN_is_zero(k2)){
        if (
            !BN_rand_range(k2,n) ||
            !BN_copy(k3, k2)
            )
            { error(); return res; }
	}

	group = EC_GROUP_new_curve_GFp(p, a, b, bn_ctx);
	generator = EC_POINT_new(group);
	if (!generator)
		{ error(); return res; }
	if (1 != EC_POINT_set_affine_coordinates_GFp(group, generator, x, y, bn_ctx))
		{ error(); return res; }
	if (1 != EC_GROUP_set_generator(group, generator, n, NULL))
		{ error(); return res; }

	G = EC_POINT_new(group);
	P = EC_POINT_new(group);
	P1 = EC_POINT_new(group);
	Q1 = EC_POINT_new(group);
	TMP = EC_POINT_new(group);

    // if r1=0 or s1=0, error
	if (BN_is_zero(r1) || BN_is_zero(s1))
		{ error(); return res; }

	// set P1 = (p1x, p1y)
	if (1 != EC_POINT_set_affine_coordinates_GFp(group, P1, p1x, p1y, bn_ctx))
		{ error(); return res; }

	// set Q1 = (q1x, q1y)
	if (1 != EC_POINT_set_affine_coordinates_GFp(group, Q1, q1x, q1y, bn_ctx))
		{ error(); return res; }

	//u1 = e * (s1^(-1)) mod n, u2 = r1 * (s1^(-1)) mod n
	if (!BN_mod_inverse(tmp1, s1, n, bn_ctx) ||
		!BN_mod_mul(u1, e, tmp1, n, bn_ctx) ||
		!BN_mod_mul(u2, r1, tmp1, n, bn_ctx) ||
		!BN_mod(u1, u1, n, bn_ctx) ||
		!BN_mod(u2, u2, n, bn_ctx)
		)
		{ error(); return res; }

	//u1*G + u2*P1 = (x', y')
	if (!EC_POINT_mul(group, TMP, u1, P1, u2, bn_ctx))
		{ error(); return res; }

	if (!EC_POINT_get_affine_coordinates_GFp(group, TMP, xprime, yprime, bn_ctx))
		{ error(); return res; }

	//verify r1 = x' mod n
	if (!BN_mod(xprime, xprime, n, bn_ctx))
		{ error(); return res; }

	if(BN_cmp(r1,xprime))
		{ error_partial_verify(); return res; }

	//k2*G + k3*Q1 = (x1, y1)
	if (!EC_POINT_mul(group, TMP, k2, Q1, k3, bn_ctx))
		{ error(); return res; }

	if (!EC_POINT_get_affine_coordinates_GFp(group, TMP, x1, y1, bn_ctx))
		{ error(); return res; }

	//r=(e+x1) mod n
	if (!BN_mod_add(r, e, x1, n, bn_ctx))
		{ error(); return res; }

	if (BN_is_zero(r))
		{ error(); return res; }
	strncpy(res.r, BN_bn2hex(r), 2*SM2LEN+1);

	//s2 = d2 * k3 mod n, s3 = d2 * (r+k2) mod n
	if (!BN_mod_mul(s2, d2, k3, n, bn_ctx) ||
		!BN_mod_add(tmp1, r, k2, n, bn_ctx) ||
		!BN_mod_mul(s3, d2, tmp1, n, bn_ctx) ||
		!BN_mod(s2, s2, n, bn_ctx) ||
		!BN_mod(s3, s3, n, bn_ctx)
		)
		{ error(); return res; }
	printf("s2: %s\n",BN_bn2hex(s2));
	printf("s3: %s\n",BN_bn2hex(s3));
	strncpy(res.s2, BN_bn2hex(s2), 2*SM2LEN+1);
	strncpy(res.s3, BN_bn2hex(s3), 2*SM2LEN+1);

    // flag2 的格式如下：flag2{xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx}，大括号中的内容为 16 进制格式（字母小写）的 d2。
    print_flag2(d2);

    rv = 0;
    BN_CTX_free(bn_ctx);

    return rv;
}

// 计算公钥P
int getPublicKey(char *str_d2, char *str_p1x, char *str_p1y) {
    int rv = 1;
    BIGNUM *negone, *a, *b, *p, *n, *x, *y;
    BIGNUM *d2, *p1x, *p1y, *px, *py;
    BIGNUM *tmp1, *tmp2;
    EC_GROUP *group;
    EC_POINT *generator, *G, *P, *P1;

    BN_CTX *bn_ctx = BN_CTX_new();
    BN_CTX_start(bn_ctx);
    if (!bn_ctx) {
        error();
        return 1;
    }

    negone = BN_CTX_get(bn_ctx);
    a = BN_CTX_get(bn_ctx);
    b = BN_CTX_get(bn_ctx);
    p = BN_CTX_get(bn_ctx);
    n = BN_CTX_get(bn_ctx);
    d2 = BN_CTX_get(bn_ctx);
    x = BN_CTX_get(bn_ctx);
    y = BN_CTX_get(bn_ctx);
    p1x = BN_CTX_get(bn_ctx);
    p1y = BN_CTX_get(bn_ctx);
    px = BN_CTX_get(bn_ctx);
    py = BN_CTX_get(bn_ctx);
    tmp1 = BN_CTX_get(bn_ctx);
    tmp2 = BN_CTX_get(bn_ctx);

    if (
        !BN_hex2bn(&d2, str_d2) ||
        !BN_hex2bn(&p1x, str_p1x) ||
        !BN_hex2bn(&p1y, str_p1y) ||
        !BN_hex2bn(&a, "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC") ||
        !BN_hex2bn(&b, "28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93") ||
        !BN_hex2bn(&p, "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF") ||
        !BN_hex2bn(&n, "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123") ||
        !BN_hex2bn(&x, "32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7") ||
        !BN_hex2bn(&y, "BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0")
    ) {
        error();
        return 1;
    }
    group = EC_GROUP_new_curve_GFp(p, a, b, bn_ctx);
    generator = EC_POINT_new(group);
    if (!generator) {
        error();
        return 1;
    }
    if (1 != EC_POINT_set_affine_coordinates_GFp(group, generator, x, y, bn_ctx)) {
        error();
        return 1;
    }
    if (1 != EC_GROUP_set_generator(group, generator, n, NULL)) {
        error();
        return 1;
    }

    G = EC_POINT_new(group);
    P = EC_POINT_new(group);
    P1 = EC_POINT_new(group);

    // set P1 = (p1x, p1y)
    if (1 != EC_POINT_set_affine_coordinates_GFp(group, P1, p1x, p1y, bn_ctx)) {
        error();
        return 1;
    }

    //P = ((d2)^(-1)) * P1 - G
    if (!BN_zero(tmp1) ||
        !BN_one(tmp2) ||
        !BN_mod_sub(negone, tmp1, tmp2, n, bn_ctx)
    ) {
        error();
        return 1;
    }
    if (!BN_mod_inverse(tmp1, d2, n, bn_ctx) || !EC_POINT_mul(group, P, negone, P1, tmp1, bn_ctx)) {
        error();
        return 1;
    }

    if (!EC_POINT_get_affine_coordinates_GFp(group, P, px, py, bn_ctx)) {
        error();
        return 1;
    }
    printf("Px: %s\n", BN_bn2hex(px));
    printf("Py: %s\n", BN_bn2hex(py));

    rv = 0;
    BN_CTX_free(bn_ctx);

    return rv;
}

int main(int argc, char *argv[]) {
    int rv = 1;
    if (server(argv[1], argv[2], argv[3], argv[4], argv[5], argv[6], argv[7])) {
        error();
        return rv;
    }

    rv = 0;
    return rv;
}

这一题要求是把d2给求出来，我们知道

$s_2 = d_2 * k_3 (mod n)$

$ s_3 = d_2 * (r+k_2) (mod n)$

关键在于

1
BN_copy(k3, k2)

所以显然d2是可以解出来的

$(s_3-s_2)*r^{-1}=d_2(mod n)$

非常简单。

1
2
3
4
5
6
7
8
r=0xB9D9723CBD74689FE2CAD8BEA57DE7158202D0890F72FA611403871BC7377DDA
s2 = 0x02A20FDB2CDA53DF42F73E5C2FEADEC1E490C429779826405455E0720AE2F909
s3 = 0x3348A503A5A5CD3E9ED119232B82374CCF7411BFBEA1A3B2F3CA6CD5281BC917
n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
from Crypto.Util.number import inverse

d2 = ((s3 - s2) * inverse(r, n)) % n
print(hex(d2))

flag3

生成一个公私钥对，用公钥注册，复制签名公钥得到的证书进行登录，但是登录用户名写 shangmibeiadmin 就能拿到 flag3。

当时是队友直接去gmssl的test.py找的一个公私钥对，现在想想还是有点难绷。

（暂无截图，大概就是一个简单的交互界面，要求给用户名和证书

flag4

然后得到一个总经理.zip，要求解开加密的流量，flag4就在流量里。

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
from gmssl.sm4 import CryptSM4, SM4_ENCRYPT, SM4_DECRYPT

MULTIPLIER = 6364136223846793005
ADDEND = 1
MASK = 0xffffffffffffffff
ITERATIONS = 1000

# 从文件中读取seed
def read_seed(file_path):
    with open(file_path, 'r') as file:
        seed = int(file.read().strip(), 16)
        print("seed:", hex(seed))
    return seed

global_seed = read_seed('seed.txt')

def genRandom():
    global global_seed
    # print("global_seed", hex(global_seed))
    for _ in range(ITERATIONS):
        global_seed = (global_seed * MULTIPLIER + ADDEND) & MASK
    return (global_seed >> 32) & 0xffffffff

# 16进制字符串转bytes
def HexStringToBytes(hex_str):
    return bytes.fromhex(hex_str)

# bytes转16进制字符串
def BytesToHexString(byte_seq):
    return byte_seq.hex()

def genSM4KeyOrIV():
    return HexStringToBytes(''.join(f'{genRandom():08x}' for _ in range(4)))

def SM4Encrypt(data_bytes, key_bytes, iv_bytes):
    sm4 = CryptSM4()
    sm4.set_key(key_bytes, SM4_ENCRYPT)
    return sm4.crypt_cbc(iv_bytes, data_bytes)

def SM4Decrypt(cipher_bytes, key_bytes, iv_bytes):
    sm4 = CryptSM4()
    sm4.set_key(key_bytes, SM4_DECRYPT)
    return sm4.crypt_cbc(iv_bytes, cipher_bytes)


print("############ SM4 Cryptographic Services Start... ###################")

iv_bytes = genSM4KeyOrIV()
print("iv hex:", BytesToHexString(iv_bytes))

key_bytes = genSM4KeyOrIV()
print("key hex:", BytesToHexString(key_bytes))

# 从test.pcapng读取数据并加密
with open('test.pcapng', 'rb') as f1:
    plain1_bytes = f1.read()
    cipher1_bytes = SM4Encrypt(plain1_bytes,key_bytes,iv_bytes)

# 写密文数据到cipherText.dat
with open('cipherText.dat', 'wb') as f2:
    f2.write(cipher1_bytes)

# 从cipherText.dat读密文数据
with open('cipherText.dat', 'rb') as f3:
    cipher2_bytes = f3.read()
    plain2_bytes = SM4Decrypt(cipher2_bytes,key_bytes,iv_bytes)

# 解密密文并将明文写入到plainText.pcapng(含flag4)
with open('plainText.pcapng', 'wb') as f4:
    f4.write(plain2_bytes)

可以发现，iv和key的生成依赖线性同余，但是如果要爆破可能的随机数种子需要爆破2**32，最后当然是狠狠的爆破了（

（爆破没什么好写的就不写了

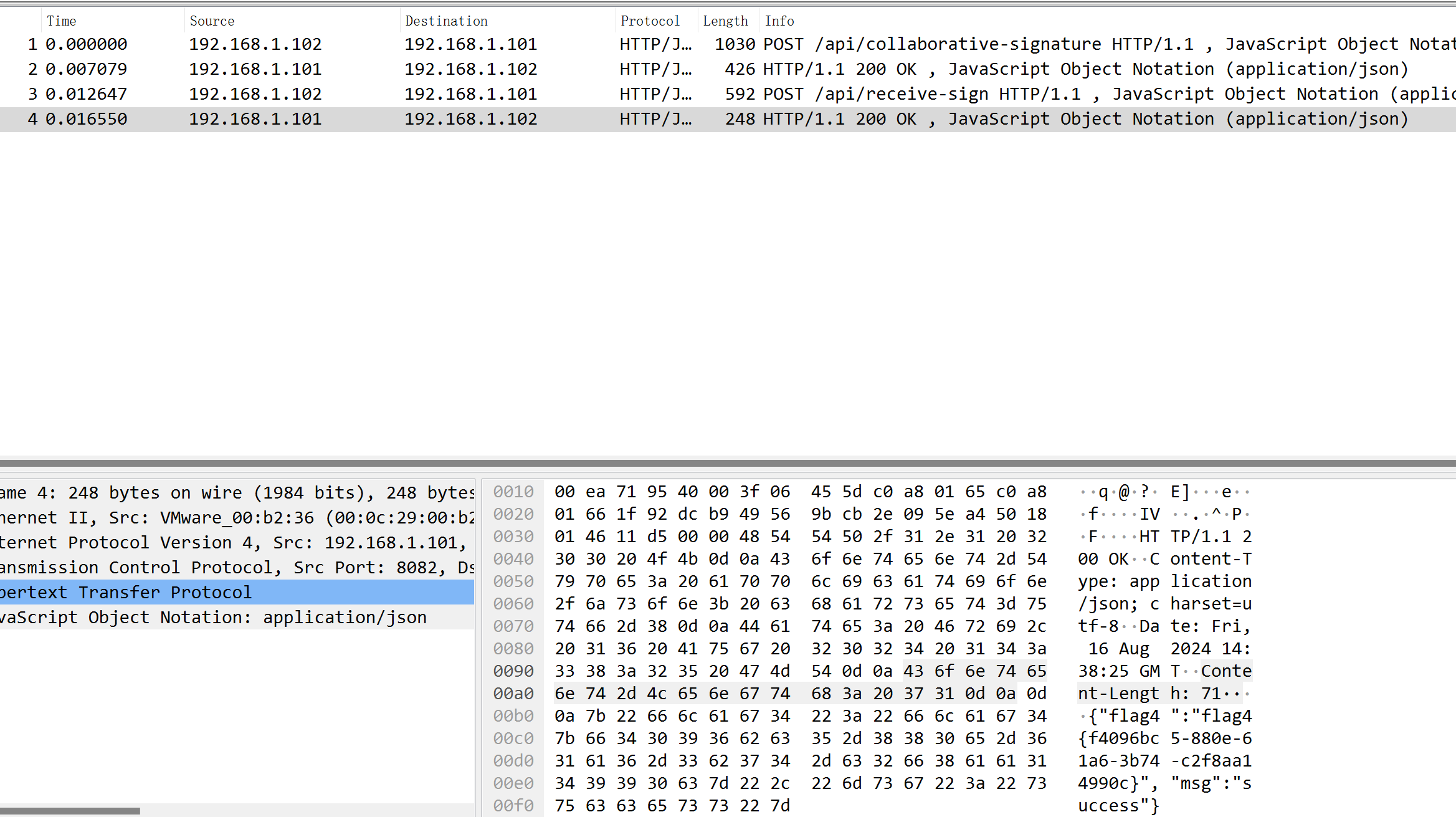
image-20240905145811936

最后得到flag4

最终挑战

最终挑战，给定一个消息摘要，要求伪造总经理的签名。

其实我们有两个方程，d1和k1都是算得出来的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
# G = GF(n)
# P.<x,y> = PolynomialRing(G, order='lex')
# # x = d1
# # y = k1
# r1 = 0x8A6BB033033E79683E81FE36D6394262D451A3DB9D1A0C489D51543D22E67BC4
# e = 0xeaf0adee014bd35a12180bbc99292e3acf895203aa97f8dbbb760da04da844f6
# s1 = 0x47baaef61c7a3c4c239fc2634ec25a2059d937026c6e0b72df1463fbba5b3a05
# s = 0xcb524f49515c9a7387210ddcdbf1f32aad1c8806f01a362c62a5d6a5466da158
# s2 = 0xB54A6668F644EC08D925552D45F66E348762B460693E7A68CBB0FDF38327DB45
# s3 = 0xB50FAE013594F79192898FF7FC0A84D931B1EC56EF9174159023ACF1C708180D
# r = 0x8A6BB033033E79683E81FE36D6394262D451A3DB9D1A0C489D51543D22E67BC4
# I = Ideal([x * e + r1 - y * x * s1, s + r - x * y * s2 + x * s3])

# I.variety()

# d = {x: 57380008957341971613717690318294399953338921752138841512102949164866741871341, y: 113664965550405303122855944928778451946027085473011499438955455126429316351741}
d1 = 57380008957341971613717690318294399953338921752138841512102949164866741871341
k1 = 113664965550405303122855944928778451946027085473011499438955455126429316351741

（这个结果应该是算的不对的 懒得再跑了

但是当时时间太紧，没看到用他给定的消息摘要值去伪造而是用了流量包里的。。

所以最后并没有做出来，最后的步骤大概是用给定的消息摘要值通过他的步骤去伪造这个签名，嗯。

如果后续找到别人的wp，会及时更新。

#CTF #Crypto #Web
2024-熵密杯-wp-Crypto
https://py-thok.github.io/2024/09/05/2024-熵密杯-wp-Crypto/
作者
PYthok-Ptk
发布于
2024年9月5日
许可协议