IEEE754协议之非数NaN——从一道活动题讲起
事情要从一道北邮百团大战的娱乐题讲起….
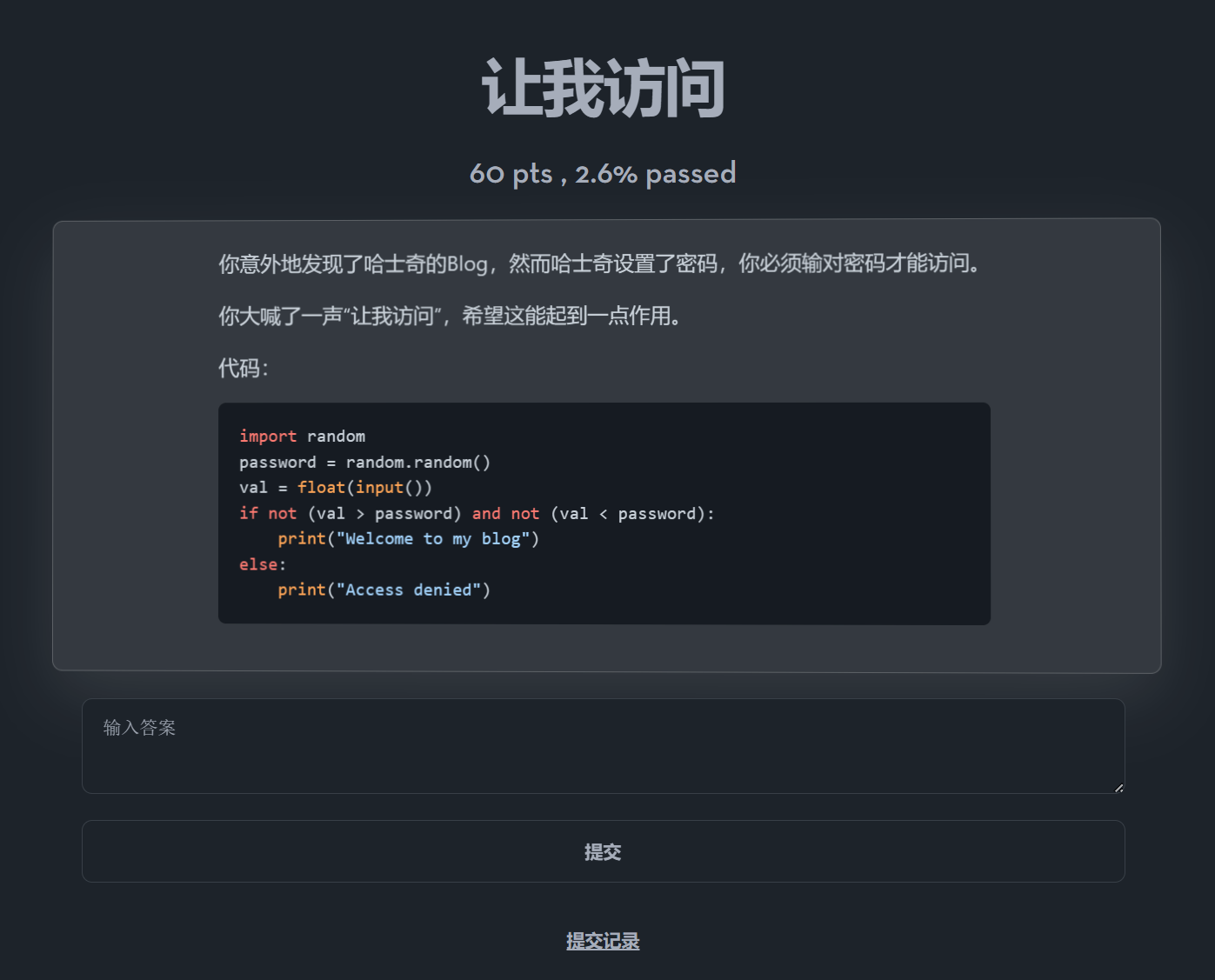
1 | |
当时我心想,娱乐题而已,应该很简单吧,结果就是做了一个下午没想出来…
中途有过多种尝试…但是还是不行…
最后纯真学长告诉我去看ieee754,我这才幡然醒悟…
实在是符合我对百团活动脑筋急转弯的刻板印象,令人感叹。
引以为戒,另外网上对于NaN的资料比较零散,我的第一篇博客就献给ieee754吧。
作者水平有限,多多包涵。XD
IEEE754是什么?
简而言之,IEEE754是一种用于二进制浮点数运算的标准,它定义了浮点数的表示方法、运算规则和格式。是美国电子和电气工程师协会(Institute of Electrical and Electronics Engineers,简称IEEE)制定的。
我们今天的主角NaN(not a number)非数,就来自于IEEE754。
IEEE 754标准定义了两种主要的浮点数格式:
- 单精度(单精度浮点数):使用32位二进制位表示一个浮点数,其中1位表示符号(正数或负数),8位表示指数(指数部分),剩下的23位表示尾数(尾数部分)。
- 双精度(双精度浮点数):使用64位二进制位表示一个浮点数,其中1位表示符号,11位表示指数,剩下的52位表示尾数。
关于IEEE754的移码,真值等详细规则,网上的大牛们已经写的很好了,我就不复制粘贴了…
NaN是什么?
NaN是未定义或无法表示的数据类型的特定值。
例如0/0通常无定义,就可以用NaN来表示。
实数域内负数平方根无解,负数对数结果复杂,反余弦/正弦定义域小于-1或大于1,亦可用NaN表示。
正负无穷大,NaN参与计算时,计算结果常常用NaN来表示。
众所周知,两个实数之间只有小于,大于,等于三种可能关系,但是一旦一个操作数为NaN时,就必须引入所谓的无序关系。
下面给出NaN与任何浮点值,NaN,正负无穷的比较。
| 比较 | NaN≥ x | NaN ≤ x | NaN > x | NaN > x | NaN = x | NaN ≠ x |
|---|---|---|---|---|---|---|
| 结果 | False | False | False | False | False | True |
显然,这道脑筋急转弯就利用了NaN与任何数做大小比较都为False的特性。
同理,在IEEE754中,NaN也是唯一一个自身不等于自身的“数”,唯一一个不等于任何数的数,需注意,与常规数学定义不同的是,float“inf“(即无穷大)也等于自身。
所以这题的答案即为NaN。
一道知识面题,会的会,不会的不会,令人感叹。
下面给出INF(无穷大)的比较。
| 比较 | INF>=x(x≠INF) | INF<=x(x≠INF) | INF>x(x≠INF) | INF<x(x≠INF) | INF=x(x≠INF) | INF≠x(x≠INF) |
|---|---|---|---|---|---|---|
| 结果 | True | False | True | False | False | True |
| 比较 | INF>=INF | INF<=INF | INF>INF | INF<INF | INF=INF | INF≠INF |
| 结果 | True | True | False | False | True | False |
持续写作,欢迎关注。